贝叶斯公式是英国学者托马斯·贝叶斯（ThomasBayes, 1702-1761）最早发现的。该结果首次发表于1763年，当时贝叶斯已经去世，而且该结果并未引起人们的重视；1774年，法国数学家拉普拉斯（Laplace）再次总结了这些结果。在之后的一段时间内，人们开始认识到贝叶斯公式的重要性，并开始利用将其广泛地应用于安全诊断、药物检测、文本识别、文件分类等。贝叶斯公式也衍生出了机器学习的一系列理论和算法，如朴素贝叶斯算法等。

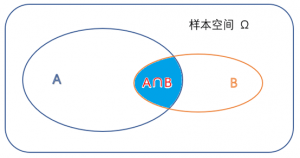
1.全概率公式

  
  从图中可以非常容易看出概率公式。

\[
P(A)=P(A|B)P(B)+P(A|\bar{B} )P(\bar{B})
\]
  从中可以推导出全概率公式。

\[
P(A)=\sum_{i}^{}P(A|B_i)P(B_i)
\]
  进一步推导出连续条件下的全概率公式。

\[
P(A)=\int_{-\infty}^{\infty}P(A|B)P(B)\mathrm{d}B
\]

2.贝叶斯定理

  
  从图中可以非常容易看出下面两个式子。
\[
\begin{align}
P(A|B)&=\frac{P(A\cap B)}{P(B)} \tag{1} \\
P(B|A)&=\frac{P(A\cap B)}{P(A)} \tag{2}
\end{align}
\]
  式子1和式子2立即可得到。
  
\[
P(B|A)=\frac{P(A|B)P(B)}{P(A)}
\]
  代入全概率公式可得到。
  
\[
P(B|A)=\frac{P(A|B)P(B)}{\sum_{i}^{}P(A|B_i)P(B_i)}
\]
  进一步推导出连续条件下的公式。

\[
P(B|A)= \frac{P(A|B)P(B)}{\int_{-\infty}^{\infty}P(A|B)P(B)\mathrm{d}B}
\]