在现实世界中,任何测量都伴随着噪声和不确定性。无论是追踪卫星轨迹、预测经济指标,还是实现自动驾驶汽车的精准定位,我们都需要一种方法从杂乱的数据中提取出真实的信号。卡尔曼滤波(Kalman Filter)正是为解决这一问题而诞生的强大工具。

鲁道夫·埃米尔·卡尔曼
在1960年,卡尔曼发表了他著名的用递归方法解决离散数据线性滤波问题的论文。从那以后,得益于数字计算技术的进步,卡尔曼滤波器已经衍生出来多种版本的滤波器。
卡尔曼滤波(kalman filter)是一种高效率的递归滤波器(自回归滤波器),如果不以人名命名,则其名称是线性二次估计(linear quadratic estimation),它能够从一系列的不完全及包含噪声的测量中,估计动态系统的状态。
扩展与变种
* 扩展卡尔曼滤波(Extended Kalman Filter)
EKF是解决非线性问题最直接、最经典的方法。它的思路很简单:在工作点附近,用线性函数来近似非线性函数。然后,就可以像标准卡尔曼滤波一样,使用线性系统的公式进行预测和更新。最后进行线性最小方差估计。
* 无迹卡尔曼滤波(Unscented Kalman Filter)
UKF采用了另一种完全不同的思路。它认为:既然函数是非线性的,我就不去线性化它,而是直接挑选一些有代表性的点(Sigma点),把这些点代入非线性函数中传播,然后通过这些传播后的点来估算新状态的均值和方差。最后进行线性最小方差估计。
算法特点
卡尔曼滤波的准则是“线性最小方差”,卡尔曼滤波“没有对分布做要求”,是一种仅挖掘“均值信息”和“协方差信息”来估计的一种方法。
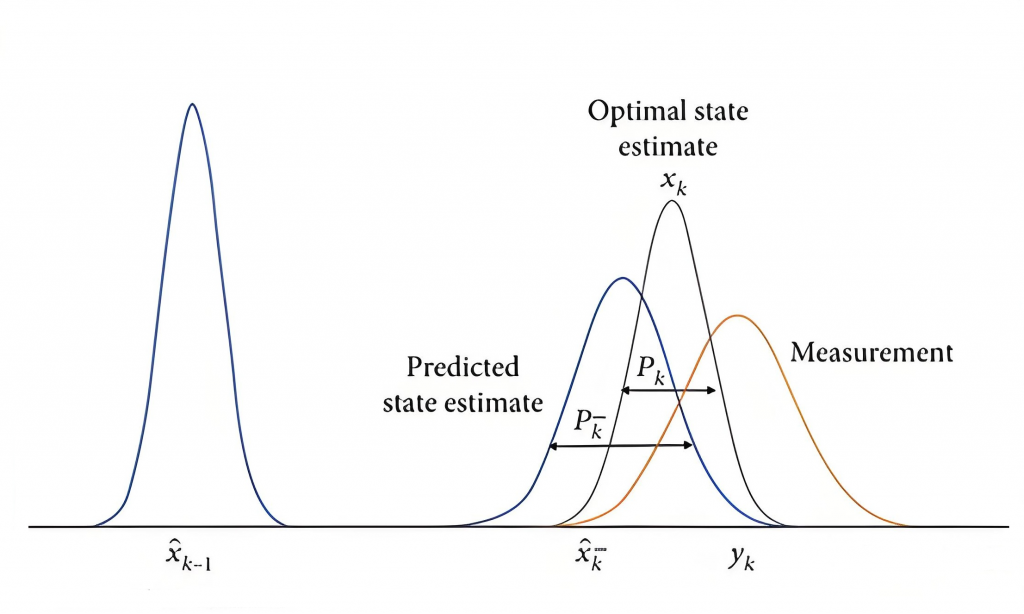
– 思想:适用于时变系统的一种估计方法,通过递推函数由“前一时刻的状态估计”获得“先验估计”,“先验估计”结合当前时刻的观测数据进行误差补偿获得“后验估计”。
– 特点:仅利用被估计量的均值和协方差矩阵,当进行线性和拟线性变换时,均值和协方差估计可以有效地保持。类似的结果不适用于分布的其他非零矩。
– 实用意义:未知分布的均值和协方差只需要维持少量恒定的信息,但这些信息足以支持大多数类型的操作活动。因此,它是计算复杂性和表示灵活性之间的成功折衷。相比之下,要完整地描述一个不断变化的误差分布,就需要保持无限数量的参数。即使有可能维护完整的概率函数信息,该信息也可能在操作上没有用处。